पाइथागोरस थ्योरम जिसे पाइथागोरस प्रमेय भी कहा जाता है, गणित का एक महत्वपूर्ण विषय है, जो समकोण त्रिभुज की भुजाओं के बीच संबंध बताता है । समकोण त्रिभुज की भुजाओं को पाइथागोरस त्रिक भी कहा जाता है। इस प्रमेय का सूत्र और प्रमाण यहाँ उदाहरण सहित समझाया गया है। पाइथागोरस प्रमेय के अनुसार, कर्ण का वर्ग त्रिभुज की अन्य दो भुजाओं के वर्गों के योग के बराबर होता है। आइए उदाहरणों के साथ पाइथागोरस थ्योरम क्या है , पाइथागोरस थ्योरम सूत्र और पाइथागोरस थ्योरम के प्रमाण के बारे में और जानें।
पाइथागोरस थ्योरम क्या है जानें
” एक समकोण त्रिभुज में, कर्ण भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है “। निम्नलिखित त्रिभुज ABC को देखें, इस त्रिभुज की भुजाओं को लम्ब, आधार और कर्ण नाम दिया गया है। यहां, कर्ण सबसे लंबी भुजा है, क्योंकि यह कोण 90° के विपरीत है। जिसमें हमारे पास कर्ण 2 = लम्ब 2 + आधार 2 ( BC 2 = AC 2 + AB 2 )है । यहां, AB आधार है, AC ऊंचाई (ऊंचाई) है, और BC कर्ण है। यह ध्यान दिया जाना चाहिए कि कर्ण समकोण त्रिभुज की सबसे लंबी भुजा है।
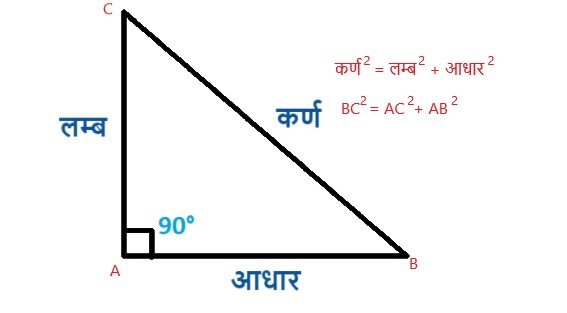
एक समकोण त्रिभुज की भुजाएँ (मान लीजिए a, b और c) जिनमें धनात्मक पूर्णांक मान होते हैं, उन्हें वर्गित करने पर एक समीकरण में डाल दिया जाता है, जिसे पायथागॉरियन त्रिक भी कहा जाता है। पाइथागोरस थ्योरम सूत्र जिसमें हमारे पास कर्ण 2 = लम्ब 2 + आधार 2 ( BC 2 = AC 2 + AB 2 )है
पाइथागोरस प्रमेय सूत्र
ऊपर दिए गए त्रिभुज पर विचार करें:
जहां “ए” लंबवत है,
“बी” आधार है,
“सी” कर्ण है.
परिभाषा के अनुसार, पाइथागोरस थ्योरम सूत्र इस प्रकार दिया गया है:
कर्ण 2 = लम्ब 2 + आधार 2
सी 2 = ए 2 + बी 2
समकोण (90°) के विपरीत भुजा सबसे लंबी भुजा होती है (कर्ण के रूप में जानी जाती है) क्योंकि सबसे बड़े कोण के विपरीत भुजा सबसे लंबी होती है।
पाइथागोरस थ्योरम के लिए उपयोगी
पाइथागोरस थ्योरम समकोण त्रिभुज की भुजाएँ ज्ञात करने में उपयोगी है। यदि हम एक समकोण त्रिभुज की दोनों भुजाओं को जानते हैं, तो हम तीसरी भुजा ज्ञात कर सकते हैं।
पाइथागोरस थ्योरम का उपयोग कैसे करें?
पाइथागोरस थ्योरम का उपयोग करने के लिए, नीचे दिए गए सूत्र को याद रखें:
सी 2 = ए 2 + बी 2 ( कर्ण 2 = लम्ब 2 + आधार 2 )
जहाँ a, b और c समकोण त्रिभुज की भुजाएँ हैं।
उदाहरण के लिए, यदि किसी त्रिभुज की भुजाएँ a, b और c हैं, जैसे कि a = 3 सेमी, b = 4 सेमी और c कर्ण है। c का मान ज्ञात कीजिये.
हम जानते हैं,
सी 2 = ए 2 + बी 2
सी 2 = 3 2 +4 2
सी 2 = 9+16
सी 2 = 25
सी = √25
सी = 5 सेमी
अतः कर्ण की लंबाई 5 सेमी है।